陽的／陰的誤差修正と折畳前処理による高速線形解法

反復解法の新しい枠組み

最近の計算機性能の進歩は目覚ましく，安価なPC上でも，ある程度の規模の3次元シミュレーションを行うことが可能になってきています。そのため様々な電気・電子機器の設計・開発の場で，計算機によるシミュレーションの果たす役割が大きくなっています。

電磁界シミュレーションにおいて広く用いられている手法の一つに有限要素法があります。有限要素法では，解析したい領域を四面体等の形状を用いて多数の小領域に分割します。

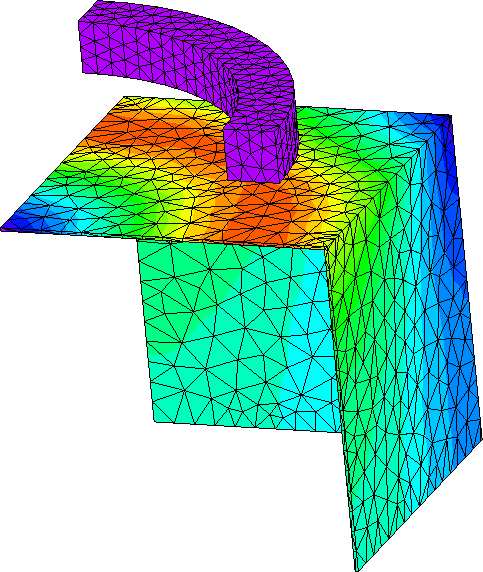
一般にこのような分割はメッシュと呼ばれます。

例えば電気スカラポテンシャルに関するポアソン方程式を解く場合であれば，メッシュの各節点におけるポテンシャルを未知数として扱います。各小領域内のポテンシャルは多項式補間によって表されると考えてください。そのように表現されたポテンシャルがポアソン方程式を近似的に満たすという条件から，メッシュの節点数と同じ個数の未知数を持つ連立方程式が導かれます。

解析の精度を向上させるためには，より細密なメッシュを用いることが必要となり，そのため上で述べた連立方程式は膨大な数の未知数を持つことになります。先端的な研究の場などでは，未知数の数が一千万から一億あるいはそれ以上となる場合もあります。進歩の著しい最近の計算機を用いたとしても，このような方程式の求解を高速に行うことは容易でありません。

本研究室では，有限要素法などで導かれる大規模な連立方程式に対する高速解法について研究・開発を行っています。最近の取組みとしては，連立方程式の反復解法の高速化に関連する

• 陰的／陽的誤差修正 (Explicit/implicit error correction, EEC/IEC)法
• 折畳前処理 (Folded Preconditioning, FP)

の提案などが挙げられます。

電磁界シミュレーションで有用とされている手法に，A－φ法・マルチグリッド法と呼ばれる手法があります。EEC/IEC法はこれらの手法を一般化した，反復解法の新しい枠組みであるといえます。EEC/IEC法を応用することで，様々な連立方程式に対して新しい高速解法を構築することが可能です。

一方FPは，連立方程式が特異（つまり無数の解を持つ）であるケースを効率的に扱うための手法です。電磁界解析できわめて広く利用されているA－φ法では，ほとんどの場合特異な連立方程式が導かれます。したがって FPを使用することによって反復解法の高速化を期待できます。

2009.2.23 更新